Lineare Regression

Wenn ein Zusammenhang zwischen der abhängigen Variablen (Zielgröße) und den unabhängigen Variablen (den beeinflussenden Prädiktorvariablen) existiert, soll die Vorhersagemöglichkeit der Zielvariablen (z.B. "Motivation") mittels multipler Regression ermittelt werden.

Bei dichotomen Größen muss die logistische Regression angewendet werden.

Beispiel zur Erklärung

Einfluss (a,b,c) zweier Einflussgrößen (2,3) auf die Zielgröße (1)

Beispiel (aus Rudolf, Müller 2004: Multivariate Verfahren):

In einem Unternehmen soll die Arbeitsmotivation der Mitarbeiter anhand von verschiedenen Merkmalen vorhergesagt werden. Neben der Zielgröße "Arbeitsmotivation" wurden Personen- und Tätigkeitsvariablen erhoben, von denen man annimmt, dass sie die Motivation beeinflussen. Diese so geannten Prädiktoren können in drei Bereiche unterteilt werden:

• Eigenschaften der Mitarbeiter:
  • Ehrgeiz
  • Kreativität
  • Leistungsstreben
• Rahmenbedingungen der Tätigkeit
  • Hierarchie
  • Lohn
  • Arbeitsbedingungen
• Inhalt der Tätigkeit
  • Lernpotential
  • Vielfalt
  • Anspruch

Ziel: Die Variable "Motivation" soll mittels multipler Regression möglichst gut vorhergesagt werden.

Voraussetzung: Es existiert ein Zusammenhang zwischen der abhängigen Variable (der Zielgröße, hier die Variable "Motivation") und den unabhängigen beeinflussenden Variablen (hier die Prädiktorvariablen).

einfache Korrelation

Streudiagramm Motivation (Y-Achse) und Leistungsstreben (X-Achse)

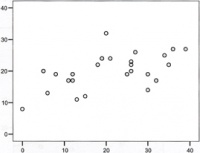
Die einfache Korrelation zwischen Motivation und Leistungsstreben ergibt folgendes Streudiagramm (siehe rechts)

Mit Hilfe von SPSS erhält man folgende Korrelationen:

		Motivation	Leistungsstreben
Motivation	Korrelation nach Pearson Signifikanz (2-seitig) N	1 25	0,559** 0,004   25
Leistungsstreben	Korrelation nach Pearson Signifikanz (2-seitig) N	0,559** 0,004   25	1 25

**Die Korrelation ist auf dem Niveau von 0,01 (2-seitig) signifikant

einfache lineare Regression

lineare Regressionsgeraden zur Vorhersage der abhängigen Variablen Motivation aus der unabhängigen Variablen Leistungsstreben

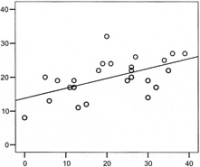
Die einfache lineare Regressionsgeraden wird mit folgender Formel errechnet: y = a + bx

"a" gibt den Schnittpunkt durch die Y-Achse an

"b" ist die Steigung der Geraden

Für unser Beispiel ergibt sich y = 13,82 + 0,29 x

Mit SPSS erhält man folgende Modellzusammenfassung:

Modell	R	R-Quadrat	korrigiertes R-Quadrat	Standardfehler des Schätzers
1	0,559	0,313	0,283	4,76831

"R" = Korrelation mit der Einflussvariablen Leistungsstreben

"R-Quadrat" = Bestimmtheitsmaß (wie gut ist Motivation durch Leistungsstreben erklärbar (in %))

Koeffizienten

Modell	nicht standardisierte Koeffizienten		standardisierte Koeffizienten	T	Signifikanz**
	B	Standardfehler	Beta
(Konstante) Leistungsstreben	13,816   0,292	2,125   0,090	0,559nbsp;	6,501   3,235	0,000   0,004

"B" = Steigung der Geraden

** Signifikanz liegt vor, wenn der Wert kleiner als 0,05 ist

Voraussetzungen

1. Gültigkeit des linearen Modells (die Punkte müssen halbwegs auf einer Geraden liegen)
2. Erwartungswert der Residuen (Abweichung von der Geraden) ist gleich Null
3. statistische Unabhängigkeit der Residuen voneinander (keine Autokorrelation)
4. Homoskedastizität (Varianz der Residuen ist unabhängig vom X-Wert. Die Streuung nimmt nicht mit der Größe der X-Werte zu)
5. bivariate Normalverteilung der Variablen x und y

Das Bestimmtheitsmaß r² dient als globales Gütekriterium der Regressionsanalyse.

r² = (erklärte Varianz / Gesamtvarianz)

r² ist in unserem Beispiel = 0,313

Zur statistischen Absicherung des Bestimmtheitsmaßes wird ein F-Test durchgeführt.

ANOVA:

Modell	Quadratsumme	df	Mittel der Quadrate	F	Signifikanz
Regression Residuen Gesamt	238,015   522,945   760,960	1   23   24	238,015   22,737	10,468	0,004

"df" = Freiheitsgrade

multiple lineare Regression

In der Regel hängt die Zielgröße nicht von einem sondern von mehreren Einflussgrößen ab. Hierbei besteht das Problem oft gerade darin, die zur Vorhersage der Zielgröße geeigneten Prädiktorvariablen auszuwählen.

Die Formel lautet hier: y = a + b1x1 +b2x2 + ...

Für unser Beispiel lautet sie:

Motivation = a + b₁ Ehrgeiz + b₂ Kreativität + b₃ Leistungsstreben + ... + b₉ Anspruch

Koeffizienten:

Modell	nicht standardisierte Koeffizienten		standardisierte Koeffizienten	T	Signifikanz**
	B	Standardfehler	Beta
(Konstante)	-3,842	5,052		-0,760	0,459
Ehrgeiz	0,193	0,081	0,337	2,381	0,031
Kreativität	0,153	0,049	0,234	3,127	0,007
Leistungsstreben	0,049	0,065	0,095	0,761	0,458
Hierarchie	0,246	0,148	0,235	1,664	0,117
Lohn	-0,001	0,001	-0,077	-0,589	0,564
Arbeitsbedingungen	-0,031	0,054	-0,045	-0,576	0,573
Lernpotential	0,165	0,098	0,199	1,683	0,113
Vielfalt	0,206	0,052	0,354	3,973	0,001
Anspruch	0,053	0,058	0,124	0,920	0,372

** Signifikanz liegt vor, wenn der Wert kleiner als 0,05 ist

Standardfehler = Streuung

standardisierte Koeffizienten = Z-Transformation

"B" = das "b" für die Formel

Somit kann in die Formel eingesetzt werden:

Motivation = -3,842 + 0,193Ehrgeiz + 0,152Kreativität + 0,049Leistungsstreben + ... + 0,053 Anspruch

Modellzusammenfassung:

Modell	R	R-Quadrat	korrigiertes R-Quadrat	Standardfehler des Schätzers
1	0,964	0,929	0,887	1,89123

R = multiple Korrelation

R-Quadrat = Bestimmtheitsmaß = Vorhersagekraft

Schlussfolgerungen

1. Beim Signifikanztest der Regressionskoeffizienten ergeben sich signifikant von Null verschiedene Regressionskoeffizienten für die Variablen "Ehrgeiz", "Kreativität" und "Vielfalt"
2. Die bisher ermittelten Regressionskoeffizienten eigenen sich für die Vorhersage und die formale Beschreibung des Zusammenhanges der unabhängigen Variablen und der abhängigen Variable.
3. Der Einfluss der Variablen "Leistungsstreben" ist mit einem Regressionskoeffizient von 0,049 deutlich kleiner als im einfachen linearen Modell (0,29). Nur die Variable "Lohn" und "Arbeitsbedingungen" haben noch kleinere Koeffizienten. Den größten Einfluss hat mit einem Koeffizienten von 0,25 die Variable "Hierarchie", obwohl diese nicht signifikant ist!!! Evtl. ist die Fallzahl zu klein oder die Einheit ist ungeschickt gewählt (vgl. Körpergröße in cm oder m)

Problem 1:

Durch unterschiedliche Einheiten wird der Einfluss der unterschiedlichen Prädiktorvariablen nicht sichtbar. Daher bedient man sich der Beta-Gewichte (siehe Tabelle oben: standardisierte Koeffizienten Beta). Somit lautet die Formel nun:

Motivation = 0,337Ehrgeiz + 0,234Kreativität + 0,095Leistungsstreben + ... + 0,124 Anspruch

Für die Vorhersage hat jetzt die Variable "Vielfalt" mit 0,354 das größte Gewicht, gefolgt von der Variablen "Ehrgeiz".

Problem 2:

Bei der Interpretation der Beta-Gewichte sind Redundanz- und Suppressionseffekte (auf Grund möglicher Korrelationen zwischen den Einflussvariablen) zu berücksichtigen.

Beispiel mit nur drei Prädiktorvariablen (Ehrgeiz, Kreativität und Leistungsstreben)

Korrelation:

	Motivation	Ehrgeiz	Kreativität	Leistungsstreben
Motivation	1,00	0,71	0,38	0,56
Ehrgeiz	0,71	1,00	0,05	0,82
Kreativität	0,38	0,05	1,00	-0,02
Leistungsstreben	0,56	0,82	-0,02	1,00

Koeffizientzen:

Modell	nicht standardisierte Koeffizienten		standardisierte Koeffizienten	T	Signifikanz**
	B	Standardfehler	Beta
(Konstante) Ehrgeiz Kreativität Leistungsstreben	5,539   0,393   0,225   0,001	2,618   0,135   0,089   0,123	0,688   0,343   0,002	2,116   2,913   2,528   0,008	0,046   0,008   0,020   0,994

Sowohl "Ehrgeiz" als auch "Leistungsstreben" korrelieren mit "Motivation". Letztere hat jedoch ein Beta-Gewicht von nahezu Null "Ehrgeiz". Die Ursache liegt in der Multikolinearität. Diese bewirkt, dass die redundante Variable "Leistungsstreben" zur Vorhersage der Zielgröße Motivation nicht mehr benötigt wird.

Modell	standardisierte Koeffizienten	T	Signifikanz	Kollinearitätsstatistik
	Beta			Toleranz	VIF
(Konstante) Ehrgeiz Kreativität Leistungsstreben	0,688   0,343   0,002	2,116   2,913   2,528   0,008	0,046   0,008   0,020   0,994	0,326   0,987   0,327	3,067   1,014   3,059

Merkmalsselektionsverfahren und hierarchische Regression

Ziel ist es, mit möglichst wenigen Einflussgrößen eine gute Vorhersage der Zielgröße zu erreichen. Das Grundprinzip der gebräuchlichen Merkmalsselektionsverfahren besteht darin, für einzelne Einflussgrößen zu beurteilen, inwieweit sich durch ihre Hinzunahme bzw. Entfernung aus dem Merkmalssatz das multiple Bestimmtheitsmaß signifikant verändert.

Merkmalsselektionsverfahren

Es lassen sich 3 prinzipielle Herangehensweisen unterscheiden:

1. schrittweise Merkmalsentfernung (Rückwärts-Verfahren)
2. schrittweise Merkmalsaufnahme (Vorwärts-Verfahren)
3. schrittweise Merkmalsentfernung bzw. -aufnahme (schrittweises Verfahren)

hierarchische Regression

Hier sind Untersuchungen über den Erklärungsbeitrag einzelner Variablen (oder Variablengruppen) (inhaltlich strukturierter Merkmalsblöcke) möglich. Das bedeutet, es kann der Frage nachgegangen werden, welchen Beitrag die beeinflussenden Größen zusätzlich zu den nicht beeinflussbaren Variablen (in unserem Beispiel "Motivation") haben.

siehe auch

• Regression (Statistik)
• logistische Regression